|
|
|
|
|
|
Jitter measurements and phase noise are not something that I would call "routine" measurements for me. I have no specialized equipment, so I have to develop it myself or find a trick how to make the measurements easy. I was lucky in this case that I found such a trick.
Note that these measurements are taken with the provisional VCXOs and must be repeated when the final ones have arrived. Also, if possible I'd like to use better equipment, particularly a better word clock generator.
Many articles have been written about jitter and I don't want to write another one here. A short introduction should do. One thing I'd like to point out are two to my point of view completely different jitter issues:
Jitter causes a mismeasurement of an actual value by an incorrect sample timing. Not the value at the intended point in time, but a different value, more or less close to that time, is measured. It is obvious that when the measured signal changes slowly this error will be less than with a fast changing signal. Also, higher amplitudes result in higher errors.
When e.g. a perfect sine wave signal is applied to an ADC and the sample timing is jittered by another, usually low-frequency sine wave signal, the converted spectrum will not only contain the original sine wave but also two spectral lines at both sides of this signal. These spectral lines look like the "side carriers" in amplitude modulation and are, in fact, close relatives of them.
The frequencies of these lateral spectral lines FJ1 and FJ2 are simply the signal's frequency FS +/- the jitter frequency FJ:
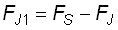 and and 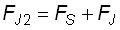 |
[1] |
|---|
The amplitude of these lateral spectral lines UJ1/2 is proportional to the signal's amplitude US, its frequency FS and the jitter amplitude TJ:
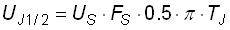 |
[2] |
|---|
or, expressed in dB:
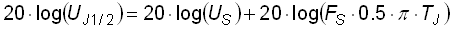 |
[3] |
|---|
|
|
which is quite exactly the measured value. |
To specify jitter as a time value only, as often can be seen, is even less useful as to specify signal-to-noise ratios in dB. For SNRs the frequency band of interest and possibly a weighting curve must be specified, too, and for jitter measurement it is even more complicated: Usually the spectral portions of signals caused by jitter are the higher the closer they are to the signal frequency, this is a very characteristical noise distribution curve.
Above, I indicated the timing error TJ caused by jitter as a time value. Phase jitter ΦJ is jitter indicated as a phase value, i.e. referenced to the clock frequency FC as ratio of the timing error to the clock's cycle time:
Phase noise is the phase jitter displayed as a spectrum in the frequency domain, normalized to a 1 Hz bandwidth. Usally either the complete spectrum is shown or a couple of numerical values at certain frequencies, e.g., 0.1 Hz, 1 Hz, 10 Hz and so on, are given.
The idea is to generate a 12 kHz tone derived from either the ADC's clock to measure the ADC's intrinsic jitter or to derive this tone from the external word clock generator in order to determine the over all jitter in a word clock synchronized ADC system. To derive the 12 kHz tone directly from the word clock signals has the advantage that, because the signal frequency is exactly synchronous to the analyzer's sample rate, a uniform FFT-window can be used. Under these circumstances the measured spectrum is ideally "sharp": There is no influence of the signal's spectral line on the neighbor one's and extreme level ratios can be displayed, no matter how close their frequencies are.
The block diagram looks like this:
When the 12 kHz divider is connected to the 48 kHz word clock reference output, the over all jitter performance of the system is determined. "Over all" means that the word clock generator's jitter is included, too. I don't have any other than a usual 24.576 MHz crystal oscillator without any jitter specification. Thus I don't know the system's performance with an ideal reference, but it can be only better than the results I got under these circumstances.
When the 12 kHz divider input is connected to ADC-IC's 48 kHz LRClk output and the VCXO runs at a fixed frequency, the jitter performance of the ADC itself is determined.
BTW, the 12 kHz divider may be a simple digital divider. There is no need to generate a sine wave signal because the low-pass filter in the ADC removes all harmonics so that for the ADC a pure sine wave signal remains. Only its amplitude should be very stable, but that's not a big challenge.
This picture shows four noise distribution curves:
Several conclusions can be drawn from these curves:
The curves above show the sidebands of +/-60 Hz from the 12 kHz test tone. The FFT resolution is 524288 points so that the spectral line resolution is 0.0915 Hz. The 12 kHz tone's level LS is -6.6 dBFS. The curves are 30 times averaged, otherwise their avarage levels wouldn't be recognizable.
The noise density must be referred to a bandwidth of 1 Hz but the measurements above refer to a spectral line resolution (SLR) of 0.0915 Hz. Thus the side band levels must be corrected by the factor of SQRT(1/SLR) = 3.3 or +10.38 dB and the for the Signal to Noise Density Ratio (SNDR) the same factor must be respected:
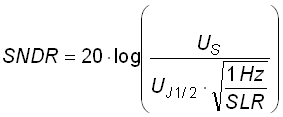
|
[4] |
|---|
The jitter density (jitter amplitude referred to a bandwidth of 1 Hz) can be derived from the equation [2] above with the SLR correction taken into account:
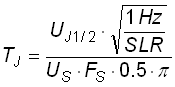 |
[5] |
|---|
and finally, with derived from equation [4]:
|
|
[6] |
|---|
Thus we can say about the over all system performance with both oscillators running and the (unknown) reference jitter included:
|
Jitter Frequency Hz |
Scale Reading dB |
Signal to Noise Density Ratio @ 12 kHz dBc/Sqrt(Hz) |
Jitter Density ps/Sqrt(Hz) |
| 0.1 | -110 | 90 | 1600 |
|
|
|
|
94 |
| 10 | -154 | 134 | 11 |
| 100 | not measurable | not measurable | not measurable |
Well, that's it. Unfortunately I don't know how other, i.e., commercial equipment looks like. Possibly this will be embarrassing for me, but I don't think so. This chapter has not ended yet. When the final VXCOs have arrived I have to do all these measurements again and maybe I'll know more by then - I'm continously learning, too.
| Last update: January, 7th, 2020 | Questions? Suggestions? Email Me! | Uwe Beis |