Resistor Noise
(= Nyquist Noise, Johnson Noise or thermal Noise)
Formula
Nomogram
Online Calculator |
Widerstandsrauschen
(= Nyquist-Rauschen, Johnson-Rauschen oder thermisches
Rauschen)
Formel
Nomogramm
Online Rechner |
|
|
Cause
Resistor noise is caused in any ohmic resistor by thermal
motion of electrons. Across the resistor a noise voltage UN
(UNoise) is generated which can be measured using
a suitable measuring instrument. In practice this noise often
limits the capability of an electronic circuit to work with particularly
low signals.
The equivalent circuit diagram of a noisy resistor is a noise-free
resistor in series with a noise voltage source: |
Ursache
Widerstandsrauschen entsteht in jedem ohmschen Widerstand
durch thermische Elektronenbewegung. Dabei entsteht eine Rauschspannung
UN (UNoise) über den Widerstand, die
mit geeigneten Messgeräten messbar ist und in der Elektronik
häufig die Fähigkeit einer Schaltung, mit besonders
kleinen Signalen zu arbeiten, begrenzt.
Schaltungstechnisch lässt sich das Rauschen eines Widerstandes
in Form der Reihenschaltung eines nicht rauschenden Widerstandes
mit einer Rauschspannungsquelle darstellen: |
 |
White Noise
Resistor noise is white noise.
That means: The noise voltage UN within a specific
measured bandwidth is independent of the frequency where the
measurement is made.
Example: When the noise of a resistor is measured whithin
a 1 Hz wide frequency band, e.g. from 1 Hz to 2 Hz,
the same measured value will arise in case of e.g. 19.999 kHz
to 20.000 kHz. It is said: The spectral density of white
noise is constant.
It can be recognized that the noise voltage (or power or current)
is not a specific value but depending on the measured bandwidth.
Specifying noise values without a specified bandwidth is nonsense!
Adding Noise Voltages
Noise generated by different sources represent signals which
have no relation to each other. These signals are called uncorrelated.
Uncorrelated signals are added by summing up the square of all
individual signals and then by extracting the root of this sum
(geometric addition). |
Weißes Rauschen
Das Widerstandsrauschen ist sogenanntes weißes Rauschen.
Das bedeutet, dass die Rauschspannung UN bei einer
bestimmten Messbandbreite unabhängig von der Frequenz ist,
bei der das Rauschen gemessen wird.
Beispiel: Wenn das Rauschen eines Widerstandes in einem 1 Hz
breiten Frequenzbereich, z. B. von 1 Hz bis 2 Hz, gemessen
wird, ergibt sich der gleiche Messwert wie bei einer Messung
von z. B. 19,999 kHz bis 20,000 kHz. Man sagt: Die
spektrale Dichte des weißen Rauschens ist konstant.
Daraus ist auch zu erkennen, dass die Rauschspannung (oder
-leistung oder -strom) kein bestimmter Wert ist, sondern immer
von einer anzugebenden Messbandbreite bestimmt wird. Die Angabe
von Rauschwerten ohne die zugehörige Bandbreite ist Unsinn!
Addition von Rauschspannungen
Rauschen aus verschiedenen Quellen sind Signale, die
keinerlei systematischen Bezug zueinander haben. Man spricht
von unkorrelierten Signalen. Unkorrelierte Signale oder Spannungen
werden addiert, indem man die Quadrate aller n Einzelspannungen
UN1 ... UNn bildet, die Quadrate addiert
und aus der Summe wieder die Wurzel zieht (geometrische Addition): |
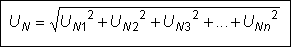 |
On the subject of geometric addition, another thought experiment: if you double a voltage, the power of the signal quadruples, as is well known. Example: If you add two sine signals of the same amplitude and frequency - does the voltage double or the power quadruple? Only if the phase of the signals is identical! If it is 180°, the voltage and the power become 0. If the frequencies are different, there is sometimes 4 times the power and sometimes 0. On average it is twice the power. Voilą - the geometric addition applies, because the two signals are not correlated.
The Influence of the Resistor Value R
When the noise voltage of a resistor of e.g. 1 Ω
is known, the noise voltage of a resistor of x Ω results
by adding the noise voltages of x resistors with 1 Ω
each. All x signals are uncorrelated and must be added geometrically.
That means: The noise voltage rises proportionally to the
square root of the resistor value.
The Influence of the Measured Bandwidth Δf
When the noise voltage of e.g. a bandwidth of 1 Hz is
known, the noise voltage of a bandwidth of x Hz results
by adding the noise voltages of x signals with a bandwidth
of 1 Hz each. Once again, as all x signals are uncorrelated they
must be added geometrically, so the noise voltage rises proportionally
to the square root of the measured bandwidth.
Example: The input noise of most op-amps is specified in V/√Hz,
i.e., the numeric value is valid for the noise for a bandwidth
of 1 Hz. Usually in audio applications the noise for the
audible bandwidth of 20 kHz is important. √(20 kHz / 1 Hz)
= 141, so the 20 kHz noise is 141 times the specified 1 Hz
noise (slightly simplified, as here the additional low-frequency
1/f noise of semiconductors is neglected, but in practice it
does not alter the result too much anyway).
The Influence of the Temperature
Because it is a thermal effect, it will obviously be depending
on the temperature, too. It also rises proportionally to the
square root of the absolute Temperature. The absolute temperature
is measured in K (Kelvin). (Absolute Zero = 0 K = -273.15°C
or -459.67°F, 0°C = 273.15 K. Because it is convenient
and useful in practice, the ambient temperature is often assumed
to be 300 K = 26.85°C = 80.33°F.) |
Zum Thema geometrische Addition noch eine Gedankenspielerei: Wenn man eine Spannung verdoppelt, vervierfacht sich bekanntlich die Leistung des Signals. Beispiel: Addiert man zwei Sinus-Signale gleicher Amplitude und Frequenz - verdoppelt sicht dann die Spannung bzw. vervierfacht die Leistung? Nur wenn auch die Phase der Signale identisch ist! Ist sie 180°, wird die Spannung und die Leistung zu 0. Sind die Frequenzen unterschiedlich, gibt es mal die 4-fache Leistung und mal 0. Im Mittel ist es die doppelte Leistung. Voilą - es gilt die geometrischeAddition, denn die beiden Signale sind ja nicht korreliert.
Der Einfluss des Widerstandswertes R
Weiß man die Rauschspannung für z. B. einen Widerstand
von 1 Ω, so ergibt sich die Rauschspannung für
einen Widerstand von x Ω indem x einzelne Rauschspannungen
für je 1 Ω addiert werden. Alle x Einzelsignale
sind unkorreliert und müssen entsprechend geometrisch addiert
werden. Das heißt, die Rauschspannung steigt mit der
Wurzel des Widerstandswertes.
Der Einfluss der Messbandbreite Δf
Weiß man die Rauschspannung für z. B. eine Bandbreite
von 1 Hz, so ergibt sich die Rauschspannung für eine
Bandbreite von x Hz, indem x einzelne Rauschspannungen für
je 1 Hz addiert werden. Alle x Einzelsignale sind wieder
unkorreliert und müssen entsprechend geometrisch addiert
werden. Das heißt, die Rauschspannung steigt mit der
Wurzel der Messbandbreite.
Beispiel: Das Eingangsrauschen der meisten Opereationsverstärker
ist in V/√Hz spezifiziert. Das bedeutet, dass der angegebene
numerische Wert für eine Bandbreite von 1 Hz gültig
ist. Üblicherweise ist in Audioanwendungen aber das Rauschen
innerhalb des Hörbereiches bis 20 kHz wichtig. √(20 kHz / 1 Hz)
= 141, also ist das 20 kHz-Rauschen 141-mal so viel wie
das 1 Hz-rauschen (etwas vereinfacht, weil hier das zusätzliche
1/f-Rauschen von Halbleitern vernachlässigt wird, wobei
es in der Praxis aber das Ergebnis auch nicht allzu sehr ändert).
Der Einfluss der Temperatur T
Da es sich um einen thermischen Effekt handelt, ist es nahe
liegend, dass er auch abhängig von der Temperatur ist und
ebenfalls mit der Wurzel der absoluten Temperatur steigt.
Die absolute Temperatur wird in K (Kelvin) angegeben werden (Absoluter
Nullpunkt = 0 K = -273,15°C und 0°C =
273,15 K. Die Umgebungstemperatur wird gerne mit 300 K =
26,85°C angenommen, weil es bequem und praxisgerecht ist.) |
|
The Formula for Resistor Noise
Respecting one remaining natural constant, the Boltzmann's
constant kB, we achieve the formula for the voltage
noise UN of a resistor R: |
Die Formel für das Widerstandsrauschen
Unter Berücksichtigung einer noch erforderlichen Naturkonstante,
der Boltzmannkonstante kB, kommt man so zur Formel
für die Rauschspannung UN an einem Widerstand
R: |
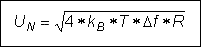 , , 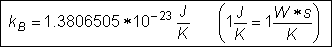 |
|
Nomogram
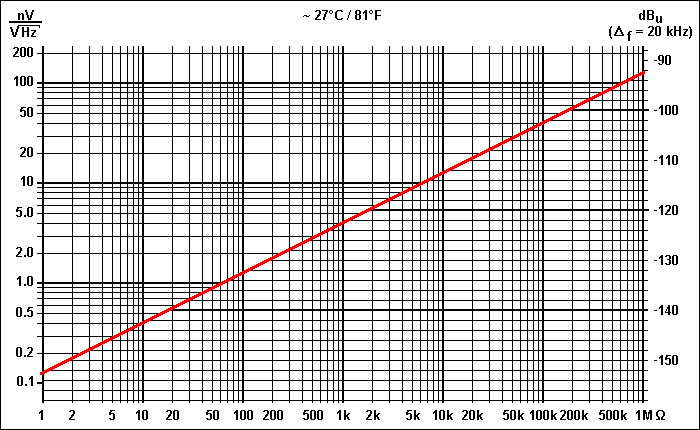
Using the following nomogram, the voltage noise for resistor
values between 1 Ω and 1 MΩ at 27°C
approx. can be evaluated, and that
- as voltage noise for a bandwidth of 1 Hz, as usually
specified, and
- as noise level in dBu for a bandwidth of 20 kHz,
as it is important for audio techniques (0 dBu
= 0.775 V).
|
Nomogramm
Im Nomogramm kann die Rauschspannung bei ca. 27°C für
Widerstandswerte von 1 Ω bis 1 MΩ ermittelt
werden, und zwar
- als Rauschspannung für eine Bandbreite von 1 Hz,
wie üblicherweise angegeben, und
- als Rauschpegel in dBu für eine Bandbreite
von 20 kHz, wie es für die Audiotechnik wichtig ist
(0 dBu = 0,775 V).
|
|
Click for an enlarged
view - Für eine vergrößerte Ansicht anklicken |
|
Some values, important and interesting in practice, are:
- 1 nV ⁄ √Hz, as much (or as low)
as the best op-amps, is produced by a resistor of 60 Ω
approx..
- 1.8 nV ⁄ √Hz are generated by
the 200 Ω approx. of a common dynamic microphone.
|
Einige für die Praxis wichtige und interessante Werte
sind:
- 1 nV ⁄ √Hz Rauschspannung, so
viel (oder so wenig) wie die besten Operationsverstärker,
wird von einem Widerstand von ca. 60 Ω erzeugt.
- 1,8 nV ⁄ √Hz werden von den ca.
200 Ω Innenwiderstand eines normalen dynamischen Mikrofons
erzeugt.
|
|
Online Calculator for Resistor Noise
(Press Enter to start calculation) |
Online-Rechner für Widerstandsrauschen
(Eingabetaste zum Start der Berechnung drücken) |
R: Ω Δf: Hz
T: °C°F
Noise Density:
nV ⁄ √Hz =
dBV ⁄ √Hz =
dBu ⁄ √Hz
Noise Level:
µV ⁄ √Δf =
dBV ⁄ √Δf =
dBu ⁄ √Δf
|
Noise Current and Noise Voltage
Up to now noise voltages where considered only. When a resistor
is shorted, a noise current flows through the resistor. It can
be calculated according Ohm's law, as usual.
Limits
At a resistor the available noise power is independent of
its resistance.Theoretically, an infite resistance produces an
infinite voltage, but with an infinite low corrent, too. In practice
the noise voltage decreases with rising frequencies, because
the parasitic capacitance parallel to the resistor together with
the resistor itself forms a low-pass filter. That is why for
very high resistances (particularly e.g. for isolators) the noise
does not matter.
Anyhow, noise is everywhere where matter is. Even in space,
though few matter can be found there. Not that one can measure
this noise with a voltmeter, but the generated noise voltages
or powers stray in form of electromagnetic fields across the
vacuum and can be received by antennas and thereby mesured out.
Here too the noise depends on the source's temperature: In space
a mean temperature of 3 k approx. (the so-called background
noise) can be gauged. When the antenna is directed towards the
sun, the noise increases significantly, theoretically up to the
value resulting from the antenna's impedance and the surface
temperature of the sun. (But this requires an antenna with such
a high directionality that, directed to the sun, only the sun
and nothing else is received.) |
Rauschstrom und Rauschspannung
Bisher wurde immer nur die Rauschspannung eines Widerstands
betrachtet. Schließt man den Widerstand kurz, so fließt
ein Rauschstrom durch den Widerstand, der sich, wie üblich,
nach dem Ohmschen Gesetz berechnen lässt.
Grenzen
Bei einem Widerstand ist die durch ihn zur Verfügung
gestellte Rauschleistung unabhängig vom Wert des Widerstands.
Theoretisch liefert ein unendlich hoher Widerstand eine unendliche
Spannung, allerdings auch mit einem unendlich kleinen Strom.
In der Praxis wird die Rauschspannung bei höheren Frequenzen
immer geringer, weil dem Widerstand immer eine parasitäre
Kapazität parallel geschaltet ist, die zusammen mit dem
Widerstand einen Tiefpass ergibt. Deshalb ist normalerweise bei
sehr hohen Widerstandswerten (insbesondere z. B. bei Isolatoren)
das Rauschen ohne Bedeutung.
Dennoch gibt es Rauschen überall, wo Materie ist. Auch
im Weltall, obwohl dort nur sehr wenig Materie zu finden ist.
Man kann zwar keine Spannung mit dem Voltmeter messen, aber die
erzeugten Rauschspannungen bzw. -leistungen vagabundieren in
Form von elektromagnetischen Feldern durch das Vakuum und können
durch Antennen empfangen und deshalb auch vermessen werden. Auch
hier ist das Rauschen abhängig von der Temperatur der Quelle:
Im Weltall ist auf diese Weise eine mittlere Temperatur von ca.
3 K zu messen (das sog. kosmische Hintergrundrauschen).
Richtet man dagegen eine Antenne auf die Sonne aus, steigt die
Rauschspannung erheblich - theoretisch auf eine Spannung, die
sich aus der Antennenimpedanz und der Oberflächentemperatur
der Sonne ergibt. (Aber das erfordert eine Antenne mit einer
so hohen Richtwirkung, dass sie, sofern sie auf die Sonne ausgerichtet
ist, nichts neben der Sonne empfängt.) |