Electronic Pages

Die Homepage der Familie Beis

Der CORDIC-Algorithmus

Der "normale Weg" und die Lösung ohne Multiplizierer zum Nachvollziehen

( English Version: The CORDIC algorithm)

Inhalt

Vorwort

Eigentlich braucht praktisch niemand mehr den CORDIC-Algorithmus. In allen Hochsprachen, allen Rechnern, allen Smartphones steht die Sinus- und Cosinus-Funktion ganz selbstverständlich als fertige Funktion zur Verfügung. Seit vielen, vielen Jahren. Wer will sich noch damit abplagen?

Ok, ich habe das getan. Zweimal sogar. In meinem DASG (Digital Audio Sine Wave Generator) habe ich ihn vor bald 10 Jahren in einem FPGA mit VHDL realisiert. Und weil ich mittlerweile schlicht und einfach vergessen hatte, wie es geht (was mich geärgert hat), wollte ich es wieder wissen. Nur deshalb habe ich mich erneut damit befasst, sonst habe ich auch keine Anwendung. Na ja, dass ein Artikel daraus entstanden ist, war es ja dann doch noch etwas wert.

Ich weiß gar nicht, ob mir das damals schon klar war: Es gibt zwei Varianten zur Berechnung von Sinus- und Cosinuswerten:

• Die eine, ich nenne sie die Sincos-Tabellen basierte Version, benötigt eine Sinus- und eine Cosinus-Tabelle mit einigen Einträgen und einen Multiplizierer zur Berechnung der Ergebnisse. Sie ist etwas einfacher zu verstehen.
• Die andere, ich nenne sie die Arctan-Tabellen basierte Version benötigt eine Arcustangens-Tabelle mit einigen Einträgen, aber keinen Multiplizierer, sondern nur Schiebe- und Additionsroutinen. Hier muss man aber etwas um die Ecke denken, um sie zu verstehen. Dafür entfallen hier die vielen erforderlichen Multiplikationen, deren Realisation in Software bei der Sincos-Tabellen basierten Version nicht nur mehr Code (oder Hardware), sondern vor allen Dingen sehr viel mehr Zeit erfordern.

Im Prinzip ist dieser Artikel überflüssig. In Wikipedia ist alles mehr als vollständig gezeigt. Nur - ich habe sehr lange gebraucht, um zumindest das Wichtigste aus dem sehr wissenschaftlich gehaltenen Artikel zu verstehen. Ich will die Kritik an der Verständlichkeit hier nicht weiter vertiefen, ich empfehle den Wikipedia-Artikel aber trotzdem, denn dort sind u. a. auch interessante historische Aspekte enthalten.

Also hatte ich mir vorgenommen, es bezüglich der Verständlich- und Nachvollziehbarkeit besser zu machen. Nachdem ich meinte, die Algorithmen zu verstehen, habe ich in Visual Basic ausprobiert, ob ich es wirklich kapiert habe. Und als das dann der Fall war, die "Königsdisziplin": Auf einem µC, der keinen Hardware-Multiplizierer hat, die Arctan-Tabellen basierte Version in Assembler zu realisieren. Zum Schluss noch die Aufbereitung meiner Erfahrungen mit diesem hoffentlich verständlichen Artikel.

Übersicht über den Algorithmus

Mit dem CORDIC-Algorithmus wird iterativ zu einem vorgegeben Winkel α (Alpha) der zugehörige Sinus- und Cosinus-Wert berechnet. Ich versuche das 1. mit Worten zu beschreiben, 2. an einer Grafik zu verdeutlichen und 3. mit einem Flussdidiagramm den genauen Rechnungsalgorithmus zu beschreiben.

Bei der Sincos-Tabellen basierten Version wird das in der folgenden Grafik mit den roten Vektoren für α = +66.66° dargestellt und geht es folgendermaßen:

1. Man fängt z. B. bei einem Winkel β (Beta) = 0 an. Dort ist cos(β) = 1 und sin(β) = 0. Das ist ein Vektor mit den Koordinaten X = 1 und Y = 0 und der Länge = 1.
2. Dann schaut man, in welche Richtung β gedreht werden muss, um α näher zu kommen.
3. Der Drehwinkel Φ (Phi) der ersten Drehung ist zu Beginn groß: 90° oder alternativ 45°. (Hier: 90°, damit lässt sich die Berechnung für die gesamten 360° in einem Durchlauf machen.)
4. β = β +/-Φ: Um diesen Drehwinkel wird gedreht: +90° oder -90° (alternativ 45°), in dieser Grafik +90°. (Bei Koordinatendrehungen bleiben die Längen der Vektoren konstant, hier = 1.)
5. Der damit erreichte Winkel β kann nach jedem Schritt größer oder kleiner als das Ziel α sein.
6. Jetzt wird der Drehwinkel Φ halbiert, also 45° (alternativ 22,5°), und es geht mit Schritt 4 in einer Schleife weiter. Dabei nähert sich β immer weiter α an, und die Werte für X und Y entsprechen immer genauer dem Cosinus bzw. Sinus von α.

Diese Schleife 4 bis 6 wird sinnvollerweise so oft wiederholt, bis die Drehwinkel Φ so klein sind, dass die Genauigkeit nicht weiter steigt, weil Zahlen nur mit endlicher Auflösung berechnet werden. Für die Koordinatendrehung werden die Cosinus- und Sinus-Werte der Drehwinkel Φ benötigt. Die müssen vorab in einer Sinus- und einer Cosinus-Tabelle zur Verfügung stehen. Außerdem werden Multiplikationen und Additionen bzw. Subtraktionen ausgeführt.

Soweit der Versuch, mit Worten einen groben Überblick über diesen CORDIC-Algorithmus zu verschaffen. Verständlicher könnte es mit dem Beispiel in der folgenden Grafik werden. In der oberen Hälfte sind für die Sincos-Tabellen basierten Version in rot die Vektoren der Iterationsschritte mit dem Startwert (X, Y) = (1 ,0) und den Winkeln β für das Ziel α = +66.66° dargestellt, wobei der Startwert und die ersten 6 Iterationsschritte mit 0 bis 6 nummeriert sind:

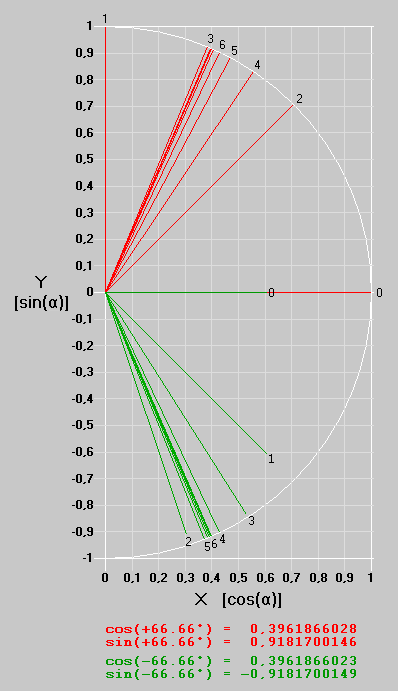
Bei der Arctan-Tabellen basierte Version ist es nicht völlig anders, aber es gibt deutliche Unterschiede. Das ist für das Ziel α = -66.66° in der unteren Hälfte der Grafik in grün dargestellt:

• Man fängt z. B. wieder bei einem Winkel β (Beta) = 0 an, aber die Länge des Start-Vektors, der gedreht wird, ist zu Anfang deutlich kleiner als 1 und erreicht gegen Ende der Iteration die erforderliche Länge 1. Es ist also keine reine Koordinatendrehung.
• Die genaue Länge dieses Start-Vektors ist von der Anzahl der Iterationsschritte abhängig, wird K genannt und und ist ca. 0,60725.
• Die erste Drehung Φ ist nur 45°, wodurch als Endergebnis = α nur etwas mehr als +/-90° erreichbar sind, sodass für +/-180° eine einfache zusätzliche Rechnung gemacht werden muss.
• Es halbiert sich nur im ersten Schritt der Drehwinkel Φ auf 22,5°, bei allen folgenden Schritten ist er immer etwas größer als die Hälfte des vorherigen Schrittes. Das hat zu Folge, dass mit diesem Verfahren prinzipiell bis zu ca. +/-99,88° berechnet werden können.
• Statt zwei Tabellen für die Sinus- und einer Cosinus-Werte wird nur eine Tabelle benötigt, die für die jeweiligen Iterations-Schritte die zugehörigen Arcustangens-Werte der Drehwinkel Φ enthält.

Der Algorithmus im Detail

Die beiden Algorithmen im Detail habe ich mal mit (m)einem weniger geeigneten, aber nicht völlig ungeeigneten Programm erstellt:

Sincos

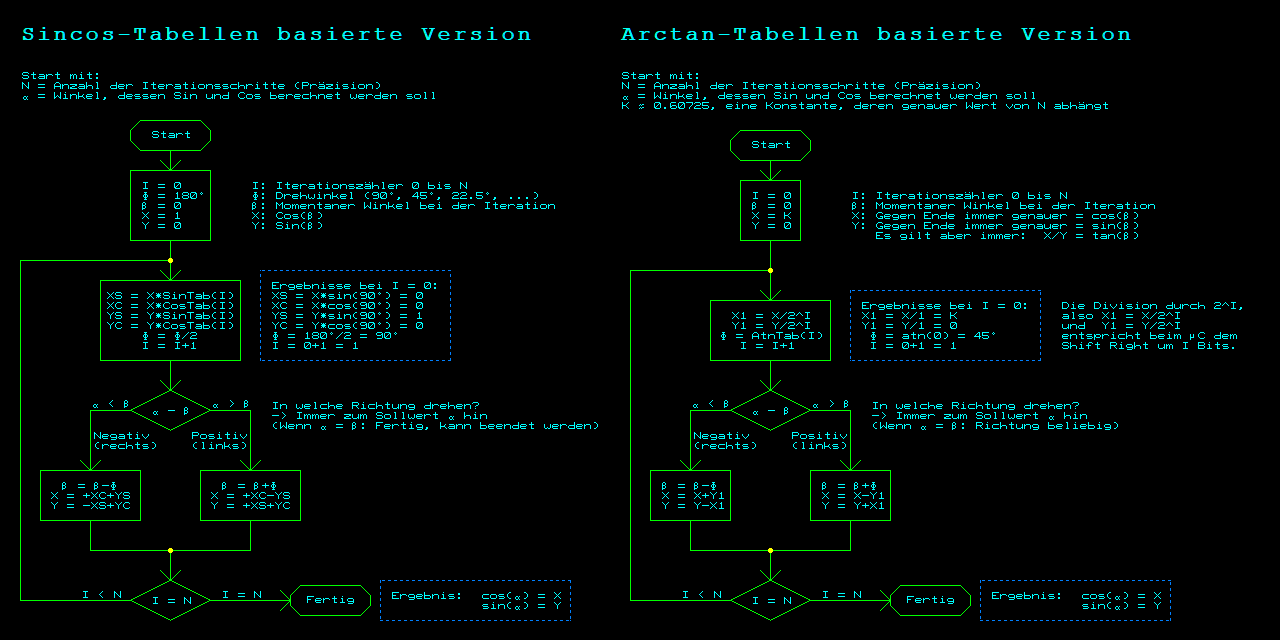
Die Sinus- und die Cosinus-Tabelle errechnet sich aus:

  SinTab(I) = sin(90°/2^I)
  CosTab(I) = cos(90°/2^I)

mit I = 0 bis zur Anzahl der Iterationsschritte N - 1 (= N Tabelleneinträge).

Arctan

Die Arcustangens-Tabelle errechnet sich aus:

  AtnTab(I) = atn(1/2^I)

mit I = 0 bis zur Anzahl der Iterationsschritte N - 1 (= N Tabelleneinträge).

Die Arcustangenstabelle für 32 Iterationsschritte sieht dann so aus:

 I      AtnTab(I)   
 0  0,78539816339745
 1  0,46364760900081
 2  0,24497866312686
 3  0,12435499454676
 4  0,06241880999596
 5  0,03123983343027
 6  0,01562372862048
 7  0,00781234106010
 8  0,00390623013197
 9  0,00195312251648
10  0,00097656218956
11  0,00048828121119
12  0,00024414062015
13  0,00012207031189
14  0,00006103515617
15  0,00003051757812
16  0,00001525878906
17  0,00000762939453
18  0,00000381469727
19  0,00000190734863
20  0,00000095367432
21  0,00000047683716
22  0,00000023841858
23  0,00000011920929
24  0,00000005960464
25  0,00000002980232
26  0,00000001490116
27  0,00000000745058
28  0,00000000372529
29  0,00000000186265
30  0,00000000093132
31  0,00000000046566

Der Faktor K korrigiert die Längenänderung des Vektors im Laufe der Iteration. K ist der Kehrwert des Produkts über alle cos(Φ) von 0 bis zum letzten angewendeten Iterationsschritt. Bei N > 24 ist K = 0,607252935008881 bzw. hexadezimal mit Wertebereich 0 bis 2^32 entsprechend 0 bis 1 ist K = 0x9B74EDA8.

Für den 32 Bit-Algorithmus in einem µC oder in anderen binär rechnenden Plattformen sähe die AtnTab(I) so aus:

.long    0x20000000   ; Φ = atn(2^ 0) = 45°
.long    0x12E4051E   ; Φ = atn(2^-1) = 26,565051177078°
.long    0x09FB385B   ; Φ = atn(2^-2) = 14,0362434679265°
.long    0x051111D4   ; Φ = atn(2^-3) = 7,1250163489018°
.long    0x028B0D43   ; Φ = atn(2^-4) = 3,57633437499735°
.long    0x0145D7E1   ; Φ = atn(2^-5) = 1,78991060824607°
.long    0x00A2F61E   ; Φ = atn(2^-6) = 0,895173710211074°
.long    0x00517C55   ; Φ = atn(2^-7) = 0,447614170860553°
.long    0x0028BE53   ; Φ = atn(2^-8) = 0,223810500368538°
.long    0x00145F2F   ; Φ = atn(2^-9) = 0,111905677066207°
.long    0x000A2F98   ; Φ = atn(2^-10) = 5,59528918938037E-02°
.long    0x000517CC   ; Φ = atn(2^-11) = 2,79764526170037E-02°
.long    0x00028BE6   ; Φ = atn(2^-12) = 0,013988227142265°
.long    0x000145F3   ; Φ = atn(2^-13) = 6,99411367535292E-03°
.long    0x0000A2FA   ; Φ = atn(2^-14) = 3,49705685070401E-03°
.long    0x0000517D   ; Φ = atn(2^-15) = 1,74852842698045E-03°
.long    0x000028BE   ; Φ = atn(2^-16) = 8,7426421369378E-04°
.long    0x0000145F   ; Φ = atn(2^-17) = 4,37132106872335E-04°
.long    0x00000A30   ; Φ = atn(2^-18) = 2,18566053439348E-04°
.long    0x00000518   ; Φ = atn(2^-19) = 1,09283026720071E-04°
.long    0x0000028C   ; Φ = atn(2^-20) = 5,46415133600854E-05°
.long    0x00000146   ; Φ = atn(2^-21) = 2,73207566800489E-05°
.long    0x000000A3   ; Φ = atn(2^-22) = 1,36603783400252E-05°
.long    0x00000051   ; Φ = atn(2^-23) = 6,83018917001272E-06°
.long    0x00000029   ; Φ = atn(2^-24) = 3,41509458500637E-06°
.long    0x00000014   ; Φ = atn(2^-25) = 1,70754729250319E-06°
.long    0x0000000A   ; Φ = atn(2^-26) = 8,53773646251594E-07°
.long    0x00000005   ; Φ = atn(2^-27) = 4,26886823125797E-07°
.long    0x00000003   ; Φ = atn(2^-28) = 2,13443411562898E-07°
.long    0x00000001   ; Φ = atn(2^-29) = 1,06721705781449E-07°
.long    0x00000001   ; Φ = atn(2^-30) = 5,33608528907246E-08°
.long    0x00000000   ; Φ = atn(2^-31) = 2,66804264453623E-08°

Es ist zu erkennen, dass der letzte Iterationsschritt mit I = 31 nicht mehr sinnvoll wäre, denn der Drehwinkel Φ ist 0. Das gleiche gilt prinzipiell auch bei einer Berechnung mit 16 Bit- oder 8 Bit-Zahlen für den letzten Schritt, also für I = 15 bzw. I = 7.

Bei weniger Iterationsschritten bzw. geringer Auflösung, z. B. bei 16 Iterationen und 16 Bit Rechengenauigkeit brauchen auch nur die ersten 16 Bit, sowohl von der Tabelle, als auch von K, sinnvollerweise gerundet, verwendet zu werden.

Fehlerbetrachtung

Es ist offensichtlich, dass die Genauigkeit der Ergebnisse von der Auflösung (Stellenzahl), mit der gerechnet wird, und von der Anzahl der Iterationsschritte abhängt. Da sich bei jeder Iteration Rundungsfehler akkumulieren, muss damit gerechnet werden, dass die letzte Stelle um mehrere Zähler falsch ist. In einem Versuch mit 32 Bit-Zahlen und 32 Iterationsschritten habe ich für ca. 30 verschiedene Winkel bei den berechneten Sinus- und Cosinuswerten Abweichungen von maximal +/-6 (von zwei Milliarden!) beobachtet. Das finde ich plausibel.

Es empfiehlt sich, für den Eingabewert α ebenso viele Bits bzw. Stellen wie für die Tabellen, die Zwischenregister und die Ausgabewerte zu verwenden.

Wertebereich

Als Winkel-Eingabe wird natürlich der gesamte 16- bzw. 32-Bit Zahlenbereich für 0 bis 360° genutzt. Also sozusagen: 360° = 0xFFFF+1.

Die Ausgabe ist ein bisschen "unangenehm": Üblich ist, mit z. B. 16 Bit den Zahlenbereich von 0 bis 65535 vorzeichenbehaftet als -32768 (0x8000) bis +32767 (0x7FFF) zu verstehen. 0x8000 skaliert als -1 für die Sinus-Berechnung wäre ja ok, aber +1 wäre dann nicht darstellbar. Denkbar wäre 0x8001 bis 0x7FFF als -1 bis +1 zu skalieren.

Bei meiner Realisierung habe ich 0x4000 als +1 und 0xC000 als -1 skaliert. Der Zahlenbereich 0x4001 bis 0xBFFF bleibt dann ungenutzt. Also 1 Bit Vorzeichen, ein Bit Vorkommastelle, 14 Bit Nachkommastellen. Das bedeutet auch, dass nicht mit K = 0x9B74EDA8, sondern einem Viertel davon, also K = 0x26DD3B6A begonnen werden muss.

Eine praktische Realisierung

Natürlich wollte ich das alles nicht nur mit Simulationen ausprobieren. Eine sinnvolle Demonstration sollte auch mit einem µC mit der Arctan-Tabellen basierten Version, also ohne Multiplizierer, laufen. Der µC ist ein MSP430Gxxxx, ein 16 Bit-µC von TI. Es sollte ein Sinussignal erzeugt werden und dessen MSByte mittels R2R-Netzwerk analog gewandelt und auf dem Oszilloskop dargestellt werden. Und ich wollte erfahren, wie groß die Berechnungszeiten für die 16 Bit- und die 32 Bit-Variante ist. Ergebnis: Bei 16 MHz Prozessortakt dauert eine Berechnung
- mit 16 Bit ca. 63 µs
- mit 32 Bit ca. 220 µs

Die meiste Zeit wird für die Schiebe-Befehle gebraucht. In der 32 Bit-Version gibt es ca. 500 davon, jeder davon braucht in einer Schleife mit Schleifenzähler und Sprung 7 Prozessorzyklen, das ergibt ca. 500*7/16 MHz = 220 µs. Ein Barrel Shifter wäre sehr hilfreich, aber den gibt es im MSP430 nicht. Immerhin kann man abkürzen, weil Schiebeoperationen größer 8 bzw. 16 teilweise durch Byte bzw. Word-Swapping und -Löschung ersetzt werden können, so ist eine Gesamtzeit von ca. 220 µs erreichbar. Mit 63 µs für eine 16 Bit-Berechnung sind sogar Sinussignale bis zu mehreren kHz in Echtzeit, z. B. für Frequenzmodulation, möglich.

Für die Demonstration habe ich die Schrittweite für jedes Sample mit 0x0055 (16 Bit-Version) bzw. 0x00550055 (32 Bit-Version) gewählt. Ein 360°-Zyklus braucht daher ~771,011 Berechnungen und dauert damit entsprechend lange. Um die erneute Quantisierung eines Digital-Scopes für Screenshots zu vermeiden, habe ich Fotos mit Langzeitbelichtung vom Analog-Scope gemacht. Zuerst die 16 Bit-Version, danach die 32 Bit-Version. Die Cursor-Linien zeigen den Betriebsspannungsbereich, von dem wegen des oben erwähnten +1-Problems nur ca. 50% ausgenutzt werden.

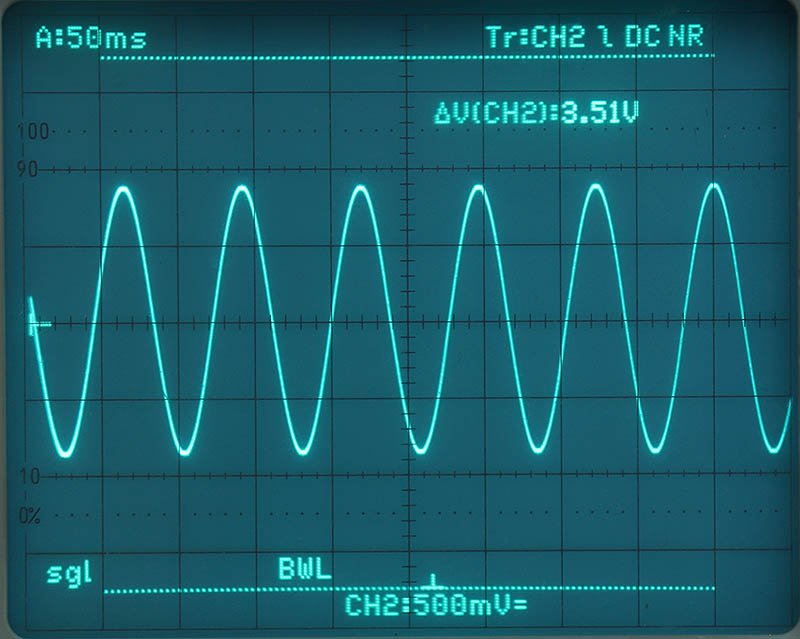
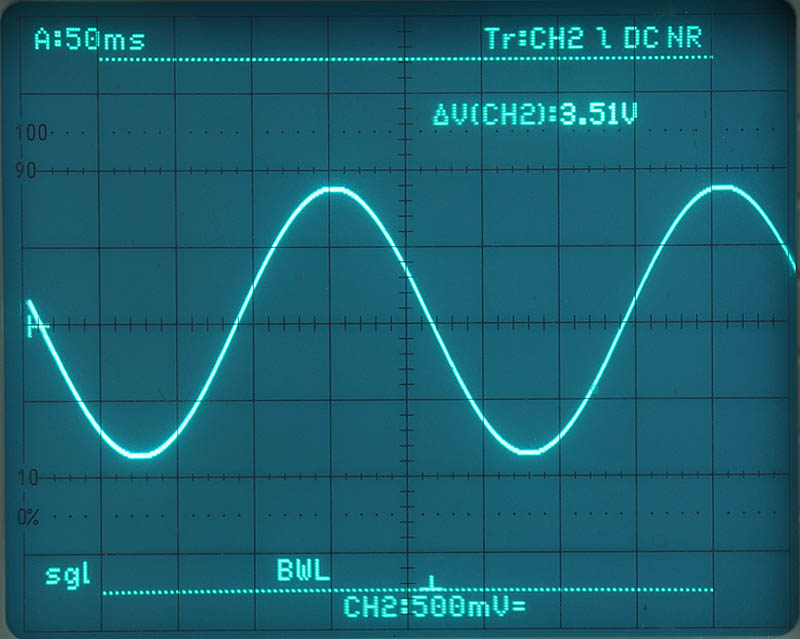
Den Code für den MSP430 veröffentliche ich hier nicht. Nicht, weil er geheim ist, sondern weil er nicht gut gepflegt ist. Aber in diesem Fall hat mir "Hauptsache, es funktioniert" ausnahmsweise einmal gereicht. Sonst halte ich diesen Spruch für das Eingeständnis des niedrigsten Anspruchs, den ein Entwickler an sich und sein Werk stellt, was ein starkes Armutszeugnis ist. Aber für die schätzungsweise 0 Personen, die sich dafür interessieren würden, wollte ich den Aufwand nicht machen, und ich selber brauche es auch nicht mehr. Sollte sich dennoch jemand dafür interessieren und sich vor nichts fürchten - lasst es mich wissen.